【第6回】 家庭でできる!数学的に考えるきっかけづくり。
2022.1.24

これからの時代を生きる力を育むために、数学とどのように関わっていけばよいのか。
本シリーズでは子どもが数学を楽しく学べるようにするために、そして子どもたちの生きる力を育むために数学で何ができるのか、全8編の連載形式でお届けします。
 東京学芸大学大学院 教育学研究科 教授 西村 圭一(にしむら けいいち)先生
東京学芸大学大学院 教育学研究科 教授 西村 圭一(にしむら けいいち)先生
東京都立高等学校、東京学芸大学附属大泉中学校、同国際中等教育学校教諭、国立教育政策研究所教育課程研究センター基礎研究部総括研究官、東京学芸大学教育学部数学科教育学分野教授を経て、現在に至る。日本数学教育学会業務執行理事、数学教育編集部長、学習指導要領等の改善に係る検討に必要な専門的作業等協力者(高等学校数学科、高等学校専門理数)、Bowland Japan代表、探究オリンピック-明日の思考力コンテスト-委員長、東京学芸大学SSH/WWL合同推進委員など多数。主な編著書に、『真の問題解決能力を育てる数学授業-資質・能力の育成を目指して』(明治図書,2016)などがある。
数学が苦手な子どもが増えている!?子どもが興味をもつ多様な数学教育とは。
家庭でできる!数学的に考えるきっかけづくり。
■「問い」を一緒に考える
身近な社会的課題に引き寄せて「数学的に考える」ことが重要ということですね。ただ、この方法だとご家庭で実践したり、アドバイスを送ったりすることの難易度が高いように思います。何かご家庭でできるようなものを教えてください。
まずは「問をもたせてあげる」ということが大切だと思います。説明まですると大変ですよね。
例えば、こちらをご覧ください。(各社の内閣支持率調査)
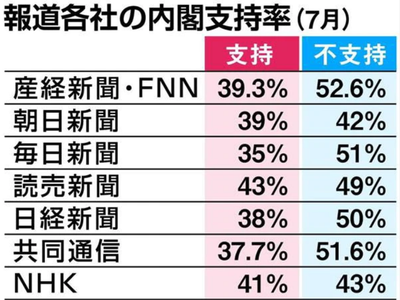
2015/7/27 THE SANKEI NEWS 『新聞主要各紙で内閣不支持率が支持率を逆転 それでも支持率4割 自民支持率も崩れず』
これはあるときの内閣支持率調査です。これをみると同じ時期に内閣支持率調査をしているのに、新聞社によって数字がことなりますよね。これをどう解釈しますか?
こういった問を子どもに投げかけるだけでも違うと思います。
例えば朝日新聞の39%と毎日新聞の35%という数字は、違いがあるのでしょうか。「4%違うじゃない」、「新聞社の傾向によって違いが出ているのではないか。」思う方もいらっしゃると思います。
しかし、これは標本調査です。すべての人に調査すれば真の支持率がわかるわけですが、そんなことはできない。だから無作為に選んで調査する,それが標本調査です。そのため,得られる結果は幅をもたせて解釈する必要があります。その幅の中にあれば新聞社による違いではないと考えなければいけません。この範囲の求め方は,高校の数学Bで学習します。数学的に求めることができるのです。
それ以外のトピックスでも同様のことが言えます。
内閣支持率の変動も2%下がると、一大事のように政治家も感じるじゃないでしょうか。しかし、この2%というのは標本調査の抽出上の誤差の範囲で、元々の支持率は変わっていない可能性が高いんです。
こういう問を「これどういう意味なの?」とご家庭で聞いてみてあげる。このようにご家庭で提起してあげて、学校へ行って数学の先生とか数学が得意な友達とかに聞いてみるということをしてほしいですね。そういう自然な会話が出てくると、数学の広がりが出てくると思います。
■海外では…
こういった問題提起は海外などでは実際にご家庭などでよくされているのでしょうか。
世界との違いという意味では博物館などに「コミュニケーター」という人がいる国が多いです。日本も「サイエンスコミュニケーター」はいますが,理科が中心ですね。
日本だと数字を示して、内閣支持率が2%あがりました、下がりましたというニュースが平然と流れていますが、本当はきちんと説明してあげないといけないですね。
コロナの感染者数の予測モデルもそうです。予想数だけが一人歩きしていましたよね。ニュース番組で,こういうモデルで,こういう仮定のもとではこのような予想になる、この仮定がこう変わるとこうなるというような説明が必要だったように思います。