【第7回】 数学はいつでも試せる実験道具だ！
2022.1.24
これからの時代を生きる力を育むために、数学とどのように関わっていけばよいのか。
本シリーズでは子どもが数学を楽しく学べるようにするために、そして子どもたちの生きる力を育むために数学で何ができるのか、全8編の連載形式でお届けします。
東京学芸大学大学院 教育学研究科 教授 西村 圭一(にしむら けいいち)先生
東京都立高等学校、東京学芸大学附属大泉中学校、同国際中等教育学校教諭、国立教育政策研究所教育課程研究センター基礎研究部総括研究官、東京学芸大学教育学部数学科教育学分野教授を経て、現在に至る。日本数学教育学会業務執行理事、数学教育編集部長、学習指導要領等の改善に係る検討に必要な専門的作業等協力者（高等学校数学科、高等学校専門理数）、Bowland Japan代表、探究オリンピック－明日の思考力コンテスト－委員長、東京学芸大学SSH/WWL合同推進委員など多数。主な編著書に、『真の問題解決能力を育てる数学授業-資質・能力の育成を目指して』（明治図書,2016）などがある。
数学が苦手な子どもが増えている！？子どもが興味をもつ多様な数学教育とは。
数学はいつでも試せる実験道具だ！
■数学的思考とは
確かに、日常生活に目を向けてみると社会課題を起点に、問をたてることができそうですね。ご家庭でも子どもだけでなく、保護者の方も疑問を持つことが大切ということですね。
これまでのお話の中で出てきた「数学的思考」というものはどういうものなのでしょうか。
何か与えられた問題に対して、正確にきちんと答えを出すことが数学的思考だと思われがちですが、これは数学的思考のほんの一部なんです。数学は答えが出てから始まるという人もいます。「なぜこの答えになるのだろう？」と疑問をもって、どの条件の影響が大きいのか、ここを変えたらどう変わっているのだろうと考えることなどです。
これが化学の実験だったら、「ここを変えたらどうなるだろう」と勝手にやったらドカーンと爆発してしまうかもしれませんよね。お金もかかりますし。数学はそういう意味では、お金がかからずに安全に実験ができて本当に楽しいと思います。
ちょっと条件や式を変えただけで、新しい発見があったりしますよ。
１つおもしろいツールを紹介させてください。これはフリーツールの「GeoGebra」というものです。
例えば、y=ax＋aという式で、aの値を変えたらグラフはどう変化しますか。
どれも点（－1，0）を通りますね。
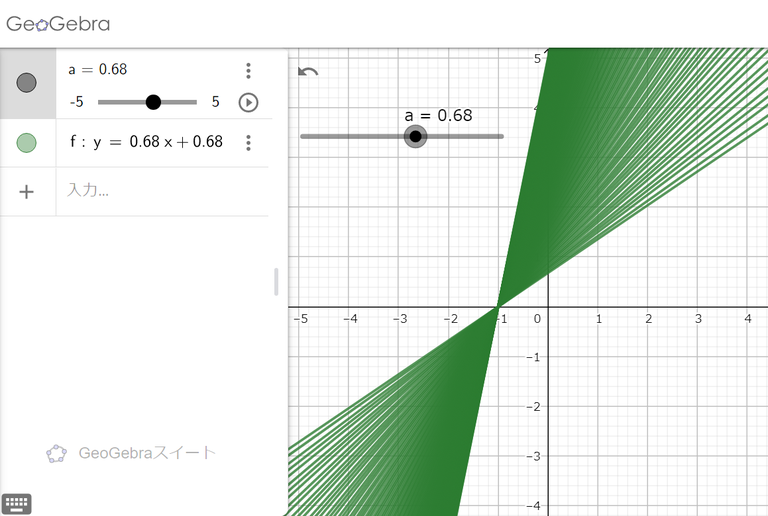
ではy=ax+ax^2としたら、どう動くとおもいますか。これは想像が難しいと思いますが、動かすとこんな動きをするんです。
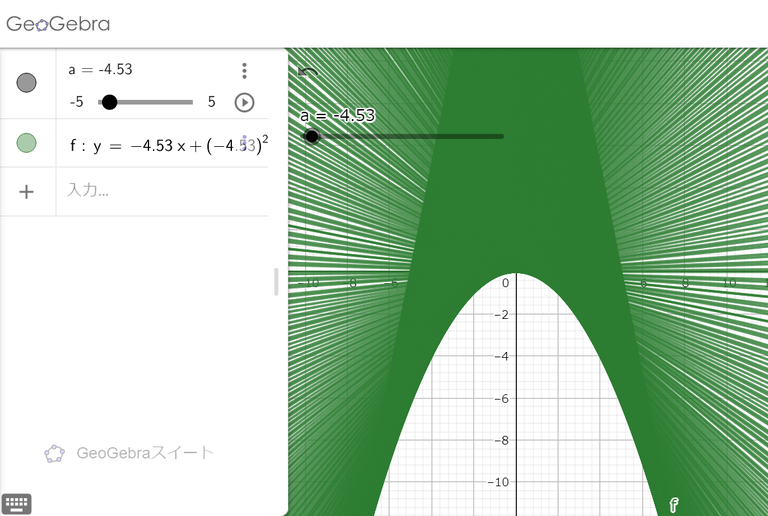
これをみると「あぁ！」となりますよね。なぜ急にこんな形が見えてくるのだろうって。
グラフが通らないところが見えますが、これを不通過領域といいます。なぜこんな形が急に出てくるのだろうと思いませんか。これは入試問題にもなり得る問です。
このように式を少し変えてみたら、おもしろい発見があって、何か見つかりますよね。それを「なぜこんな動きをするのか？」と考えることで、学びに繋がります。
さらに、こういったことをやっていくと「特別な点はないかな？」とか「特殊な条件にしてみよう」とかも考えたくなります。これらも数学的思考です。そういうことをやるとまた面白くなってくるわけです。いまは、このような考え方さえ，入試の穴埋め問題の答えを見つけるテクニックのように教えている人もいるのが現状です。それは本質的な思考とはだいぶ離れてしまっています。
